Actionables 2.0: Rational Action/Knowing yourself better

[phreakv6]

There are two things in this post - Somwhat mathematical, somewhat probabilistic and behavioral, maybe even philosophical (they are all inter-related anyway). Some things I have have been ruminating over the last few hours. The payoff from this could be useful in current markets - Or so I think.

It started with this puzzle I received in a whatsapp group.

“There is a long line of people waiting outside a theatre to buy tickets. The theatre owner comes out and announces that the first person to have a birthday same as someone standing anywhere before him in the line gets a free ticket. Where will you stand to maximize your chance?”

This is a very simple-sounding puzzle where the brain naturally thinks that standing further back in the queue increases our chances of a sure win (More birthdays to choose from, for your position) - For eg. if you stood at 366th position, you have all 365 unique days to choose from - Surefire win - But at what cost? As you go further back, hoping for the high probability of a sure win, you also give others a chance to have a go - For eg. A person at 365th position has 364/365 birthdays to choose from and a very, very high chance of winning. So you must optimise and find an appropriate position. Where will that position be? What’s the number that your brain intuitively comes up with? Mine said somewhere in the middle - Say around 180 should be good for me. Am neither too greedy, nor too fearful at 180. Right?

So I set myself down to solving the puzzle and optimising for both variables and what I found was completely non-intuitive (Unless my solution is wrong, in which case, please PM me).

These are screenshots from my iPython notebook.

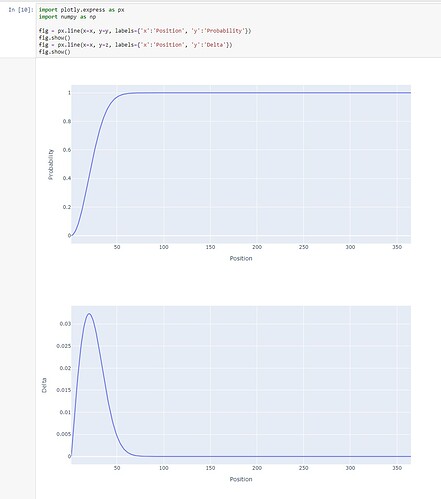
The answer to the puzzle is 20. Yes, you must stand in position 20, if you are not too greedy or fearful as your brain claims yourself to be. This is where the probability is 0.5 for winning. This is also the position where the incremental increase in probability in moving back in the queue, maximizes out. This is completely un-intuitive to our brain as standing in position 20 sounds like a losing proposition.

So what happens if you stood at position 20 and you lost? There is still 50% chance of losing here. Handle it with equanimity, as you merely played the odds the way it should be played. What happens if you win? Hand over the credits to lady luck and take credits for computing the odds.

Standing anywhere after about position 50 to position 365, makes hardly any difference, probablistically speaking. Between 20-50 is the juice is.

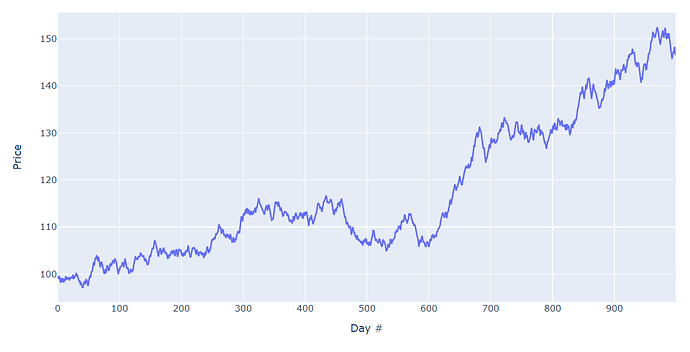
This is just like waiting for a market bottom, where you wait for great deals, giving reasonable deals a pass - reasonable deals which should at least probably be nibbled upon, while prepping yourself up for the great deals, if they do come - Again, let me be very clear that this would be overfitting a bivariate distribution to a multi-variate problem with a lot of uncertainties. But the concept is fairly similar and the takeaway should only be that our brain’s intuitive position in something like this, probably should not be trusted. Our brain is good at optimizing for one variable and it is very good at loss aversion and it is very good at holding onto a decision - all of these, most times in a combination can be harmful, despite our best efforts.

So how do you decide?

I have been using Kelly Criterion reasonably successfully for asset allocation based on risk:reward. Under uncertainty though, computing risk:reward is a fools errand. This is where I came across Minimax Regret from a post on Epsilon Theory earlier this week. The idea is fairly simple - You choose the course of action where you minimize your maximum regret. If you think that the course of the market running away from you is going to cause you maximum regret, you avoid that course - by buying a bit. If you think that market making bigger bottoms is going to be your maximum regret, you minimize it by not going all in - The point is, you don’t take either path if you think both will lead to maximum regret. This doesnt take into account external probabilities but works solely based on you and so will have different courses for different horses. Ruminate on that.

[nil_71]

That’s why Vijay Kedia Sir always says…please know yourself 1st. Then invest

Investing is simple…but many a time…we complicate things …

[parkhi_nazar]

Dear phreak,

This was a very nice read. I’ve been through this journey (incl. the knowing yourself part and the use of “regret minimization” which I’ve been following and recommending for some years now). I will add just one more nuance, based on personal experience.

Let me start off by saying that the regret minimization framework, partnered with good financial analysis skills is a very powerful combination - because it enables you to work with your personality. That alone is good enough for a person to do very well in the markets.

At the same time, there is always room for improvement. To improve upon a regret minimization framework, it is helpful to analyze how this framework has helped or hurt you in the past. The main step here is reflecting if you make any systematic errors in your judgement. For example, is your personality such that you are prone to sitting on the sidelines and not acting OR are you prone to jumping in too early when markets are tanking? On the whole, you may be following a regret minimization framework. For e.g. The “jumping in too early guys” will buy when share price falls below their estimate of fair value (including a margin of safety). They may be okay taking the pain of more downside - because of their conviction. The person with a tendency to jump in too early will typically regret “missing the bus” more than “taking it on the chin”. As I said before, they may be doing well overall with this strategy.

However, if you realize that you are the type of personality that systematically ends up jumping in too early, it may be worth adjusting for that factor. And hold on to more dry powder. Doing this can make a good performance better. This is extremely tough to do, because it goes against your grain (and it also goes against the regret minimization framework). That is why a true and objective reflection of your tendency for systematic errors is important. And then (sigh!) that most difficult step of acting on it.

[vinoths]

@phreakv6 - Thanks for sharing your thoughts. I can relate similar thought-process from my recent read - The Little Book of Behavioral Investing by James Montier.

It seems a food for thought on “actionables” to prepare, plan and execute disciplined way in the coming weeks/months. Here is the relevant excerpt from the book,

[phreakv6]

One of the most important aspects I have been ruminating on for the last couple of years is the chasm between ‘knowing’ and ‘doing’. This is the primary cause behind someone saying something and doing something else - What causes this inconsistency in behavior? Why is it so widespread? ‘Acta, non verba’ (Deeds, not words) captures the essence of this - ‘Talk is cheap’ is the modern version.

In investing, this manifests itself in being able to freely quote greats - like ‘The time to buy is when there’s blood in the streets’ (Rothschild) but shirk and cower when the time to act presents itself. So clever is the brain that it neglects rationality and starts rationalizing (vastly different, these two) - that the intelligence often becomes self-defeating.

This manifests sometimes in people in positions of power preaching something and acting to the contrary. There is a 16th century saying as well to this effect - ‘Do as I say, not as I do’ - ‘Stop giving me gyan and show me what’s in your portfolio’ is the investing version of it to deal with the hypocrisy. How are we so good at deluding ourselves and deluding others? It is perhaps not intentional for the most part and yet it is so common.

Our brain’s neocortex perceives patterns and stores what is learned through its neurons. Real learning comes when several positive and negative effects learned through an “experience” comes together and several sets of neurons fire together and hence wire together (Hebbian learning). This makes the learning well and truly etched in the pathways of brain leading to consistent behavior.

When people learn from the experiences of others or from books, the learning is vicarious and vicarious learning is easy to parrot, hard to follow unless behavior is forcefully dissected and debugged which is extremely hard and time-consuming.

So when someone says something and does something else, their belief systems embedded in their neural pathways isn’t yet attuned to that learning and they are probably in a phase of transition where there is a cognitive dissonance between existing beliefs and newly learned and sometimes contradictory beliefs. This is why it is very easy to learn fresh than re-learn as this contradiction is minimal.

In summary, the cognitive dissonance that leads to the chasm between knowing and doing can be bridged but its not easy. If you keep the dissonance healthy - Don’t pick sides, even if it is for the moment (It is very easy to delude yourself once you do) - The dissonance exists because both or several options feel ‘right’ and they very well might be, based on the probabilities for the outcomes. The most rational thing to do would be to act in a way that doesn’t kill the dissonance - so the next time someone sounds like a hypocrite, understand that they took the easy way out of a conflict.

[diffsoft]

This is a brilliant insight on the question to why the gap between what people say and what they do, something that I have been curious about too.

When I studied the biographies of some of the great leaders, esp Lincoln, I observed that they keep an active dissonance until the last microsecond almost.

Must have taken a lot of work for you to put it so succinctly. Thank you!

[zygo23554]

@phreakv6

How are we so good at deluding ourselves and deluding others? It is perhaps not intentional for the most part and yet it is so common.

Delusion & denial are mostly unconscious else they would not work. If this weren’t the case, some part of the brain knows what the truth is and delusion/denial cannot perform their function.

The smart cookie projects a facade of tactical denial using plausible deniability as a plank. This is an example of manipulative self awareness.

The not so smart cookie is not even aware of what is happening because he/she does not see any incentive to understand own behavior. Which is why it never occurs to a hypocrite that he/she might be one. It is not a lie if you believe it.

You either get it or you don’t, there is nothing in between. Once you get it, you cannot go back to not getting it, this is the curse of smartness.

[Alok16]

Hi @phreakv6 Thanks for this, was an extremely interesting read, Could you please share some texts/ resources could read up on such problems, this methodology employed etc

( I am quite interested in the MINMAX theorem and the logic employed to solve such problems would really appreciate links etc)

Thanks
Alok

[phreakv6]

Another one of those computational meditations. This time on geometric random walks.

Simple piece of code (Notebook on github & live version on binder)

Some price charts generated by the above code (Randomly picked. If you run the above, you will find several like these)

Sample 1 - You may see a cup & handle breakout

Sample 2 - You may see a flag breakout?

As someone who has been using technical analysis reasonably successfully, when combined with some rudimentary fundamental analysis, this is a bit of challenge for me. Chart after chart, my trained eye found patterns in a jiffy even though I know there isn’t any.

Charts above use (-1,+1.1) - to account for optimism and earnings, the thing that makes stocks go up in the long term. When playing with the parameters a bit, to make the range something like (-1,+1), the charts are very different though its just a 0.1% difference in range (power of compounding in the geometric random walk).

Sample 3 - Drifting downwards and appearing to break the downtrend

Sample 4 - Meandering and making an all time high

There are a lot of charts on a similar vein with the range bound to (-1,+1). If you extend the simulation, they will most likely not make you money, no matter how optimistic they may look in the shorter term.

So that lead me thinking - What were these small characteristics (range being the one here) that generate these endless snowflakes of uniqueness? Earnings, predictability of it, certainty of it and longevity of the certainty?. Some businesses can easily be slotted as (-0.9,1) ones that you don’t want to touch, (-1,+1) businesses that flatter to deceive and some as (-1,+1.1) where you want to be.

In the short term, several (-1,+1) businesses can have a brief range shift but one must never get carried away and get stuck in these (high likelihood in current environment). The thread starter was written from the depths of a scary bear market. The environment since has made us all feel like geniuses and take undue credit (going by posts on twitter). Its time to take a moment and respect the randomness and be conscious of bad habits that we may have inevitably picked up in good times.